Funzione digamma

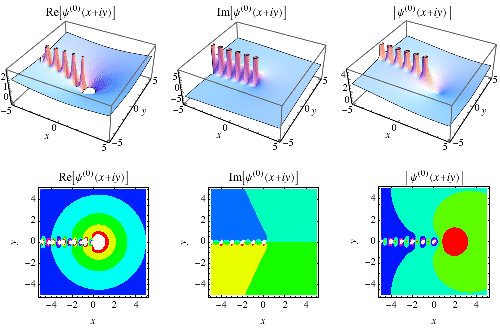
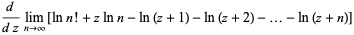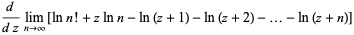In matematica, per funzione digamma si intende la funzione speciale definita come derivata logaritmica della funzione gamma:

${\displaystyle \psi _{0}(x):={\frac {\operatorname {d} }{\operatorname {d} x}}\ln {\Gamma (x)}={\frac {\Gamma '(x)}{\Gamma (x)}}.}$

La funzione digamma talora viene anche denotata con ${\displaystyle \Psi (x)}$ e talora anche ${\displaystyle \psi ^{0}(x)}$. Essa è collegata ai numeri armonici dalla uguaglianza

${\displaystyle \psi _{0}(n)=H_{n-1}-\gamma }$

dove ${\displaystyle H_{n-1}}$ denota l'${\displaystyle (n-1)}$-esimo numero armonico e ${\displaystyle \gamma }$ è la ben nota costante di Eulero-Mascheroni. Tale relazione si dimostra dalla definizione alternativa di Gauss della funzione gamma

${\displaystyle \Gamma \left(s\right)=\lim _{n\rightarrow \infty }{\frac {n!n^{s}}{s\left(s 1\right)\left(s 2\right)\ldots \left(s n\right)}},}$

da cui

${\displaystyle \psi \left(s\right)={\frac {d}{ds}}\lim _{n\rightarrow \infty }\left(\ln n! s\ln n-\ln s-\ln \left(s 1\right)-\ln \left(s 2\right)-\ldots -\ln \left(s n\right)\right)}$

${\displaystyle \psi \left(s\right)=\lim _{n\rightarrow \infty }\left(\ln n-{\frac {1}{s}}-{\frac {1}{s 1}}-{\frac {1}{s 2}}-\ldots -{\frac {1}{s n}}\right)}$

${\displaystyle \psi \left(s\right)=\lim _{n\rightarrow \infty }\left(\ln n-\sum _{k=1}^{s n}\left({\frac {1}{k}}\right) 1 {\frac {1}{2}} \ldots {\frac {1}{s-1}}\right)}$

${\displaystyle \psi \left(s\right)=\lim _{n\rightarrow \infty }\left(\ln n-\sum _{k=1}^{n}\left({\frac {1}{k}}\right)\right) 1 {\frac {1}{2}} \ldots {\frac {1}{s-1}}}$

${\displaystyle \psi \left(s\right)=-\gamma H_{s-1}.}$

Invece, se l'argomento della funzione digamma non è un numero intero positivo, ma è un generico numero complesso ${\displaystyle z}$, si dimostra che

${\displaystyle \psi _{0}(z)=\psi \left(z\right)=-\gamma -{\frac {1}{z}}-\sum _{k=1}^{\infty }\left({\frac {1}{z k}}-{\frac {1}{k}}\right).}$

Bibliografia

• (DE) N. Nielsen Handbuch der Theorie der Gammafunktion (Teubner, 1906) p. 15
• (EN) T. M. MacRobert Functions of a Complex Variable (McMillan, 1917) p. 161
• (EN) M. Abramowitz e I. Stegun Handbook of Mathematical Functions (US Governement Printing Office, 1964) p. 258

Voci correlate

• Funzione G di Erdelyi
• Funzione gamma
• Funzione poligamma
• Numero armonico

Altri progetti

• Wikimedia Commons contiene immagini o altri file sulla funzione digamma

Collegamenti esterni

• Funzione digamma, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.
• (EN) Eric W. Weisstein, Digamma Function, su MathWorld, Wolfram Research.
• (EN) Psi-function, su Encyclopaedia of Mathematics, Springer e European Mathematical Society.
• Polygamma function in functions.wolfram.com